本节书摘来自华章出版社《 线性代数及其应用 (原书第4版)》一书中的第1章,第1.7节,作者:(美)戴维C. 雷(David C. Lay)马里兰大学帕克学院 著刘深泉 张万芹 陈玉珍 包乐娥 陆 博 译,更多章节内容可以访问云栖社区“华章计算机”公众号查看
1.5节的齐次线性方程组也可从另一观点研究,即把它们写成向量方程. 这时,重点从Ax=0 的未知数的解转向出现在向量方程中的向量.例如,考虑方程 (1)此方程当然有平凡解,即 ,如1.5节,主要问题是,平凡解是否是唯一解.定义 中一组向量 称为线性无关的,若向量方程
仅有平凡解. 向量组(集) 称为线性相关的,若存在不全为零的权 ,使 (2)方程(2)称为向量 之间的线性相关关系,其中权不全为零. 一组向量为线性相关,当且仅当它不是线性无关的. 为简单起见,我们也可说 线性相关,意思是向量组(集) 是线性相关组. 对线性无关组也使用类似的语言.例1 设
确定向量组 是否线性相关.可能的话,求出 的一个线性相关关系.解 a. 我们需要确定方程(1)是否有非平凡解,把增广矩阵进行行变换,得显然, 和 为基本变量, 为自由变量. 的每个非零值确定(1)的一组非平凡解,因此 线性相关.
为求出 的线性关系,继续化简增广矩阵,写出新的方程组
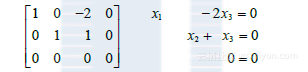故 为自由变量. 选取 的一个非零值,比如 ,则 ,把这些值代入(2)得
这是一个(无穷多个之中的一个)可能的线性相关关系. 矩阵各列的线性无关设我们考虑矩阵 ,矩阵方程 Ax=0可以写成 A的各列之间的每一个线性相关关系对应于方程Ax=0 的一个非平凡解. 因此我们有下列重要事实.矩阵A 的各列线性无关,当且仅当方程Ax=0 仅有平凡解.例2 确定矩阵 的各列是否线性无关.解 研究 Ax=0,把增广矩阵行变换:此时,显然方程有3个基本变量,没有自由变量,因此方程Ax=0 仅有平凡解, A的各列是线性无关的. 一个或两个向量的集合仅含一个向量,比如说由 v形成的集合线性无关当且仅当v不是零向量. 这是因为当 时向量方程 仅有平凡解. 零向量是线性相关的,因 有许多非平凡解.下列例子说明两个向量线性相关的情况.例3 确定下列向量组是否线性无关解 a. 注意 是 的倍数,即 . 因此-2v1+v2=0,表明 线性相关.
和 的任意一个不是另一个的倍数. 它们能否线性相关?设c 和 d满足若 ,我们可用 表示 ,即 ,这是不可能的,因 不是 的倍数. 故 c必是零. 类似地 d必是0,于是 是线性无关组. 例3中的讨论说明,你总可以用观察法来决定两个向量是否线性相关. 行变换是不必要的,只要看一个向量是否是另一个向量的倍数即可(这个方法只能用于两个向量的情况).两个向量的集合 线性相关,当且仅当其中一个向量是另一个向量的倍数. 这个集合线性无关,当且仅当其中任一个向量都不是另一个向量的倍数. 从几何意义上看,两个向量线性相关,当且仅当它们落在通过原点的同一条直线上. 图1-30表示例3中两组向量的情况.两个或更多个向量的集合下面定理的证明类似于例3的思路. 详细的证明在本节末给出.定理7 (线性相关集的特征)两个或更多个向量的集合 线性相关,当且仅当 S中至少有一个向量是其他向量的线性组合,事实上,若 S线性相关,且 ,则某个 它前面几个向量 的线性组合.警告 定理7没有说在线性相关集中每一个向量都是它前面的向量的线性组合,线性相关集中某个向量可能不是其他向量的线性组合. 见练习题3.例4 设 ,叙述u 和 v生成的集合,并说明向量 w属于Span{u,v} 当且仅当{u,v,w} 线性相关.解 向量u 和 v是线性无关的,因为它们之中任何一个不是另一个的倍数,所以它们生成 中一个平面(见1.3节),事实上, Span{u,v}就是 平面(即 ),若 w是u 和v 的线性组合,由定理7知 {u,v,w}线性相关,反之,设 {u,v,w}线性相关,由定理7知{u,v,w} 中某一向量是它前面的向量的线性组合(因 ),这向量必是 w,因为 v不是u 的倍数. 因而w 属于 Span{u,v},见图1-31. 例4可推广到 中任意集合{u,v,w} ,其中 u与 v线性无关. 这时集合 {u,vw}线性相关当且仅当w 在 u和v 所生成的平面上.下面两个定理说明了线性相关的一些条件. 定理8在今后各章中是一个关键的结果.定理8 若一个向量组的向量个数超过每个向量元素个数,那么这个向量组线性相关. 就是说, 中任意向量组 ,当 p > n时线性相关.证 设 ,则 A是n*p 矩阵,方程对应于 p个未知量的n个方程,若 p>n,未知量比方程多,所以必定有自由变量. 因此Ax=0 必有非平凡解,所以A 的各列线性相关,图1-32给出了这个定理的矩阵说明. 警告 定理8没有涉及向量组中向量个数不超过每个向量中元素个数的情形.例5 向量 线性相关. 因为每个向量仅有2个元素而共有3个向量,注意:其中任何一个向量并不是另一向量的倍数. 见图1-33. 定理9 若向量组 包含零向量,则它线性相关.证 把这些向量重新编号,我们可设 ,于是方程 证明了S 线性相关. 例6 用观察法确定下列向量组是否线性相关.解 a. 这个向量组包含4个向量,每个向量仅有3个元素,因此它们线性相关.
定理8不能应用,因为向量个数不超过每个向量中元素个数. 因该组中有零向量,根据定理9,因此它线性相关.若我们比较两向量的对应元素,第2个向量看来是第一个向量的-3/2倍. 这个关系对前3对元素成立,但对第4个不成立. 因此,这两向量中任意一个不是另一个的倍数,因此是线性无关的. 一般地,你必须把每一节完整地读几遍才能理解像线性相关这样的重要概念. 学习指导书中的这一节的注解对你掌握线性代数中的这一重要思想是很重要的. 例如,下列的证明值得一读,因为它指出如何应用线性无关的定义.定理7(线性相关集的特征)的证明 若S 中某个 是其他向量的线性组合,那么把方程两边减去 就产生一个线性关系,其中 的权为(-1),例如,若 ,那么于是 S 线性相关.反之,设 S线性相关,若 为零,则它是 S中其他向量的一个(平凡)线性组合. 若不为零,存在 不全为零,使设j是使的最大下标. 若j=1 则 ,这是不可能的,因 ,故 j>1. 而练习题设 .
集合{u,v} ,{u,w},{u,z},{v,w},{v,z}和{w,z} 都是线性无关的吗?为什么?练习题1的答案是否蕴涵着{u,v,w,z} 也线性无关?为确定 {u,v,w,z}是否线性相关,是否有必要验证w 是 u,v,z的线性组合?{u,v,w,z} 是否线性相关?习题1.7 相关资源:线性代数及其应用(原书第四版)习题解答