《写给程序员的数据挖掘实践指南》——5.7一个新数据集及挑战

本节书摘来自异步社区出版社《写给程序员的数据挖掘实践指南》一书中的第5章，第5.7节，作者：【美】Ron Zacharski（扎哈尔斯基），更多章节内容可以访问云栖社区“异步社区”公众号查看。

5.7一个新数据集及挑战

现在到考察一个新数据集的时候了，该数据集是美国国立糖尿病、消化和肾脏疾病研究所（United States National Institute of Diabetes and Digestive and Kidney Diseases，简称NIDDK）所开发的皮马印第安人糖尿病数据集（Pima Indians Diabetes Data Set）。

令人吃惊的是，有超过30%的皮马人患有糖尿病。与此形成对照的是，美国糖尿病的患病率为8.3%，中国为4.2%。

数据集中的每个实例表示一个超过21岁的皮马女性的信息，她属于以下两类之一，即5年内是否患过糖尿病。每个人有8个属性。

属性：

1．怀孕次数。

2．2小时口服葡萄糖耐量测试中得到的血糖浓度。

3．舒张期血压（mm Hg）。

4．三头肌皮脂厚度（mm）。

5．2小时血清胰岛素（mu U/ml）。

6．身体质量指数（体重kg/（身高in m）^2）。

7．糖尿病家系作用。

8．年龄。下面给出了一个数据的例子（最后一列表示类别：0表示没有糖尿病，1表示有糖尿病）。

2　　99　　52　　15　　94　　24.6　　0.637　　21　　0

3　　83　　58　　31　　18　　34.3　　0.336　　25　　0

5　　139　　80　　35　 160　　31.6　 0.361　　25　　1

3　　170　　64　　37　 225　　34.5　 0.356　　30　　1

因此，上例中第一位女性有过两个孩子，血糖为99，舒张期血压为52，等等。

在本书网站上有个两个文件，其中zip文件pimaSmall.zip中包含100个实例，它们分到10个文件（桶）中。而pima.zip文件则包含393个实例。当使用上一章构建的近邻分类器对pimaSmall数据集进行10折交叉验证时，会得到如下结果：

提示：Python函数heapq.nsmallest(n,list)会返回最小的n个元素构成的列表(list)。下面是你要完成的任务：

从本书网站下载分类器的代码，实现kNN算法。此时需要修改类中的initializer方法以便加入另一个参数k：

def __init__(self, bucketPrefix, testBucketNumber, dataFormat, k):

该方法的签名看起来类似于def knn(self, itemVector)：

它应该使用self.k（记住要在init方法中设置该值）并返回类别结果（在Pima癌症数据集上为0或1），还应该修改tenfold过程以便将k传递给initializer。

我对init_的修改十分简单：

def __init__(self, bucketPrefix, testBucketNumber, dataFormat, k): 　　　　self.k = k 　　　　...

我的kNN方法如下：

def knn(self, itemVector): 　　"""returns the predicted class of itemVector using k 　　Nearest Neighbors""" 　　# changed from min to heapq.nsmallest to get the 　　# k closest neighbors 　　neighbors = heapq.nsmallest(self.k, 　　　　　　　　　　　　　　[(self.manhattan(itemVector, item[1]), item) 　　　　　　　　　　　　　　for item in self.data]) 　　# each neighbor gets a vote 　　results = {} 　　for neighbor in neighbors: 　　　　theClass = neighbor[1][0] 　　　　results.setdefault(theClass, 0) 　　　　results[theClass] += 1 　　resultList = sorted([(i[1], i[0]) for i in results.items()], 　　　　　　　　　　　　　　reverse=True) 　　#get all the classes that have the maximum votes 　　maxVotes = resultList[0][0] 　　possibleAnswers = [i[1] for i in resultList if i[0] == maxVotes] 　　# randomly select one of the classes that received the max votes 　　answer = random.choice(possibleAnswers) 　　return( answer)

我对tenfold的一点点修改如下：

def tenfold(bucketPrefix, dataFormat, k): 　　results = {} 　　for i in range(1, 11): 　　　　c = Classifier(bucketPrefix, i, dataFormat, k) 　``` 　　　... 你可以从网站guidetodatamining.com上下载上述代码。记住，这只是该方法实现的一种做法，并不一定是最佳的做法。  哪种做法会带来更大的不同？是使用更多的数据（比较pimaSmall和pima上的分类结果）还是采用更好的算法（比较k=1和k=3两种情况）？  下面给出的是我得到的精确率结果（k=1时的算法就是上一章的最近邻算法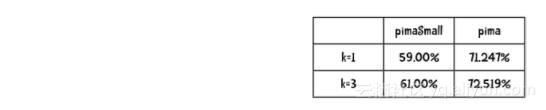）。  因此，看上去将数据规模提高到3倍所带来的精确率提高的程度高于算法带来的提高。  嗯，72.519%的精确率看起来相当不错，但是到底是不是这样呢？计算Kappa统计量来寻找答案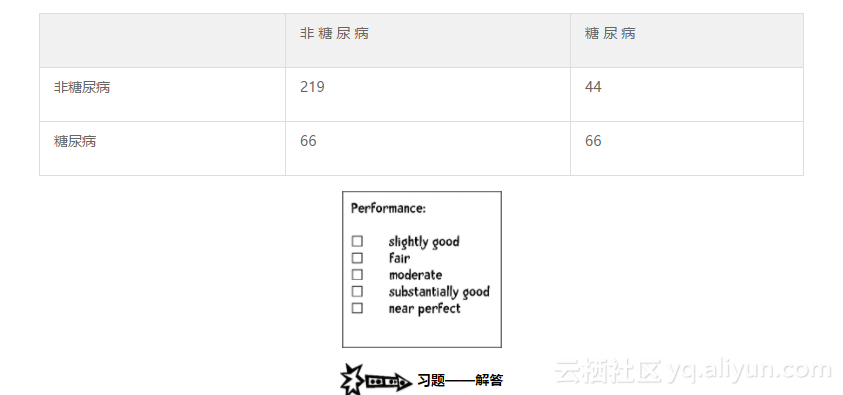：  从上面可知，这只是一个性能一般的结果。  随机(r)分类器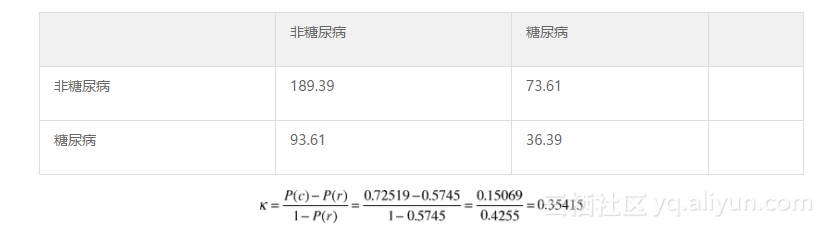：  精确率为： 相关资源：敏捷开发V1.0.pptx