【2.4.1 Mileage Bank】【问题描述】ACM(Airline of Charming Merlion,迷人的鱼尾狮航空公司)的飞行里程计划对于经常要乘坐飞机的旅客非常不错。一旦乘坐了一次ACM航班,你就可以在ACM里程银行中根据实际飞行里程赚取ACM奖励里程。而且,你可以使用ACM里程银行中的ACM奖励里程来兑换将来的ACM免费机票。下表帮助你计算当你要乘坐ACM航班的时候,可以赚取多少ACM奖励里程。
上表表明,你的ACM奖励里程由两部分组成。一部分是你的实际飞行里程(一个航班的经济舱的最低ACM奖励里程为500英里),另一部分是当你乘坐商务舱和头等舱时的飞行里程奖励(其精度可达1英里)。例如,你乘坐ACM航班从北京飞到东京(北京和东京之间的实际里程是1329英里),根据你乘坐的舱类Y、B或F分别可以奖励1329 英里、1994英里或2658英里。你乘坐ACM航班从上海飞往武汉(上海和武汉之间的实际里程为433英里),你乘坐经济舱可以奖励500英里,乘坐商务舱可以奖励650英里。请帮助ACM编写一个程序,来自动计算ACM的奖励里程。输入:输入包含若干测试用例,每个测试用例含多条航班记录,每条航班记录占一行,格式如下:出发城市 目的地城市 实际里程 舱类代码每个测试用例以包含一个0的一行结束。以包含一个#的一行表示输入结束。输出:对每个测试用例,输出一行,给出ACM奖励里程的总和。
试题来源:ACM Beijing 2002在线测试地址:POJ 1326,ZOJ 1365,UVA 2524提示本题是一道简单的直叙式模拟题:依次输入航班信息,根据每次航班的实际里程和舱类代码累计奖励里程的总和。【2.4.2 Cola】【问题描述】便利店给出以下的优惠: “每3个空瓶可以换1瓶可口可乐。”现在,你准备从便利店买一些可口可乐(N瓶),你想知道你最多可以从便利店拿到多少瓶可口可乐。图2.4-1给出了N=8的情况。方法1是标准的方法:喝完8瓶可口可乐之后,你有8个空瓶;你用6只空瓶去换,得到了2瓶新的可口可乐;喝完后你有4个空瓶,因此用3个空瓶又换了一瓶新的可口可乐。最后,你手上有2只空瓶,不能再去换到新的可乐了。因此,你一共获得8+2+1=11瓶可乐。
但实际上有更好的方法。在方法2中,先从你的朋友(或者店主)那里借一个空瓶,这样就可以获得8+3+1=12瓶可乐。当然,你要还给你的朋友你剩下的空瓶。输入:输入若干行,每行给出一个整数N (1 ≤ N ≤ 200)。输出:对于每个测试用例,程序要输出你最多可以喝到多少瓶可口可乐。你可以向别人借空瓶,但如果这样做,要确保你有足够的瓶子还给他们。
试题来源:Contest of Newbies 2006在线测试地址:UVA 11150提示设想买的可口可乐的瓶数为n;借的空瓶数为i;总瓶数为cnt,兑换前cnt=n+i;实际喝到的可口可乐瓶数为tot ,兑换前tot=n;ans为最多可喝到的可口可乐瓶数,初始时为0。反复模拟如下兑换过程,直至cnt≤3为止:
产生的空瓶数tmp=cnt%3; 增加的饮料瓶数cnt/=3; 实际喝到的饮料瓶数tot+=cnt; 总瓶数cnt+=tmp; if (cnt≥i &&tot>ans) ans=tot; // 若能偿还借来的空瓶且喝到的饮料最多, 则``` 记下由于每3个空瓶可以换1瓶可口可乐,因此只有i=0,i=1,i=2这三种情况。按照上述方法模拟这种兑换情况,最后得出的ans即为最多可喝到的可口可乐瓶数。 **【2.4.3 The Collatz Sequence】** 【问题描述】 Lothar Collatz给出的一个产生整数序列的算法如下:Step 1: 任意选择一个正整数A作为序列中的第一个项;Step 2: 如果A = 1,则算法终止;Step 3: 如果A是偶数,则用A / 2代替A,转向Step 2;Step 4: 如果A是奇数,则用3 *A + 1代替A,转向Step 2。
人们已经证明,对初始A 的值小于等于109时,这一算法会终止,但A 的有些值在这一序列中会超出许多计算机上整数类型的范围。在本题中,请确定这一序列的长度,这一序列要包括所有的值,或者算法正常终止(在Step 2),或者产生的值大于指定的限制(在Step 4)。 输入: 本题的输入包含若干测试用例。对每个测试用例,输入一行,给出两个正整数,第一个整数给出A的初始值(Step 1),第二个整数给出L,表示序列中的项的限制值。A和L都不会大于2147483647(可以在32位有符号整数类型中存储的最大值)。A的初始值总是小于L。在最后一个测试用例后的一行给出两个负整数。 输出: 对每个输入的测试用例,输出用例编号(从1开始编号)、一个冒号、A的初始值、限制值L,以及项的数量。  试题来源:ACM North Central Regionals 1998 在线测试地址:UVA 694 提示 这是一道按指令行事的直序模拟题。若初始值为a、序列中项的限制值为l,则按照下述方法计算项数ans:ans初始化为0; while(a<=l&&a!=1){ // 若当前项值不超过上限且非1,则项数+1 ans++; 根据a的奇偶性计算下一项,即a=a&1?3*a+1:a/2; } if(a==1)ans++;// 若最后一项为1,则增加1项
**【2.4.4 Let’s Play Magic!】** 【问题描述】 有一个纸牌魔术,叫“拼字蜜蜂”,过程如下: 魔术师首先将13张纸牌放置成一个圆形,如图2.4-2所示。 <p style="text-align:center">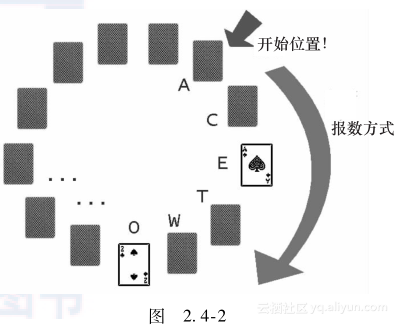 </p>1)从标志的位置开始,按顺时针对纸牌进行报数,说“A-C-E”。 2)然后将E位置的纸牌翻转过来,在图2.4-2中是纸牌中的A(Ace)。 3)接下来,将这张A拿走,继续报数,说“T-W-O”。 4)然后将 O位置的纸牌翻转过来,在图2.4-2中是纸牌中的2(Two)。 5)他对剩下的纸牌继续这样做,剩下的纸牌从3(Three)到大王(King)。 现在要问,魔术师会如何放置这些纸牌? 输入: 输入由多个测试用例组成。每个测试用例首先给出一个整数N(1≤N≤52),表示在魔术中使用的纸牌的数量。接下来的N行给出纸牌翻转的次序以及被拼写的单词,没有单词会超过20个字符。每张纸牌的格式是两个字符的字符串:第一个是值,第二个是纸牌的花色。 输入以N=0结束,这一测试用例不用处理。 输出: 对每个测试用例,输出纸牌的初始放置次序。 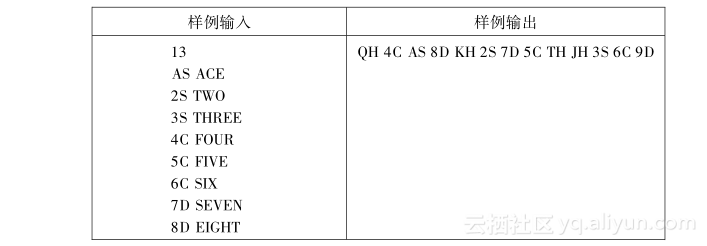 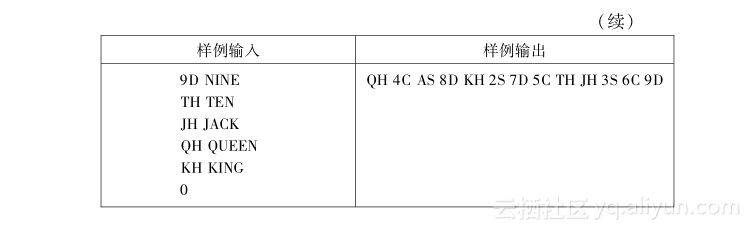 试题来源:Return of the Newbies 2005 在线测试地址:UVA 10978 提示 设第i张纸牌的格式为card[i],被拼写的单词为word[i],初始的放置次序为order[i]。模拟魔术师的动作,按如下方法复原纸牌初始的放置次序order[]: 1)顺推每张牌i(0≤i≤n-1)。 2)从第i-1张牌初始的位置j出发,沿顺时针方向数strlen(word[i])张牌。若该位置j(=(j+ strlen(word[i])-1)%n)未确定初始放置次序,则order[j]=card[i]。 ** 【2.4.5 Throwing cards away !】** 【问题描述】 给出一副已经排好序的n张纸牌,编号从1到n,编号为1的纸牌在顶,编号为n的纸牌在底。只要这副纸牌至少还有两张纸牌,就执行下述操作: 将顶部的纸牌丢弃掉,然后将此时在顶部的牌移到底部。 请编写程序,给出丢弃纸牌的序列,以及最后留下的纸牌。 输入: 输入的每行(除了最后一行)给出一个整数n ≤ 50,最后一行给出0,程序不用处理这一行。 输出: 对于输入的每一个数字,输出两行。第一行给出丢弃的纸牌的序列,第二行给出最后留下的那张纸牌。在每一行没有前导和后继空格。见样例的格式。  试题来源:A Special Contest 2005 在线测试地址:UVA 10935 提示 按题目所描述的进行模拟,模拟采用的数据结构为队列。设队列的首尾指针为p、t。初始时p=1,t=n;每张牌的后继指针为next[],初始时next[i]=i+1(1≤i≤n-1)。 进行n-1次操作,其中第i次操作为: 1)丢弃的牌编号为p。 2)将次顶的牌移到底部(next[t]=next[p]; t=next[t]; p=next[t])。 最后留下的牌编号为t。 **【2.4.6 Gift?!】** 【问题描述】 在一个小村庄里有条美丽的河。n块石头从1到n编号,从左岸到右岸以一条直线排列: [左岸]—[Rock 1]—[Rock 2]—[Rock 3]—[Rock 4]…[Rock n] — [右岸] 两块相邻的石头之间的距离正好是1米,左岸和Rock 1以及Rock n和右岸的距离也是1米。 青蛙Frank要过河,他的邻居青蛙Funny来对他说:“喂,Frank,儿童节快乐!我有个礼物给你,你看见了吗?在Rock 5上的一个小包裹。” “啊!太好了!谢谢你,我这就去取。” “等等……这份礼物只给聪明的青蛙,你不能直接跳到那里去取。” “啊?那么我应该做什么?” “要跳多次,首先你从左岸跳到Rock 1,然后,无论向前还是往后,你想跳几次就跳几次,但你第i次跳必须达到2*i-1米。更重要的是,一旦你返回左岸或到达右岸,游戏结束,你就不能再跳了。” “呣,这不容易……让我考虑一下。”青蛙Frank答道,“我可以试一下吗?” 输入: 输入给出不超过2000个测试用例。每个测试用例一行,给出两个正整数n(2≤n≤106)和m(2≤m≤n),m表示放置礼物的石头的编号。以 n=0, m=0的测试用例终止输入,程序不必处理这一测试用例。 输出: 对每个测试用例,如果可以到达Rock m,则输出一行“Let me try!”;否则,输出一行“Don't make fun of me!”  注意: 在第2个测试用例中,Frank可以以下述方法去取礼物:向前(到rock 4),向前(到rock 9),向后(到rock 2),取得礼物! 如果Frank在最后一跳向前跳,那么它就跳上了右岸(本题设定右岸足够宽阔),也就输掉了这场游戏。 试题来源:OIBH Online Programming Contest 1 在线测试地址:ZOJ 1229,UVA 10120 提示 可以用数学方法证明:当n≥50时,所有地方都可以跳到;若n≤50 ,需搜索计算可行性。由于是测试数据组,因此我们先离线计算出该范围内所有河宽可达位置的情况: 一般可采取记忆化搜索的方法计算ans[][]。以后每输入一对n和m,如果n≤50,则可根据ans[][]表中对应元素的值直接回答。 **【2.4.7 A-sequence】** 【问题描述】 一个A序列(A-sequence)是一个由正整数ai组成的序列,满足1 ≤ a1 < a2 < a3 <… ,并且序列中每个ak不是序列中早先出现的两个或多个不同项的和。 请编写一个程序,确定给出的序列是不是一个A序列。 输入: 输入由若干行组成,每行先给出一个整数D(2 ≤ D ≤ 30),表示当前序列的整数个数。然后给出一个序列。序列由整数组成,每个整数大于等于1,并且小于等于1000。输入以EOF结束。 输出: 对每个测试用例,输出两行:第一行给出测试用例编号和这一序列;如果相应的测试用例是一个A序列,则第二行输出“This is an A-sequence.”;如果相应的测试用例不是一个A序列,则第二行输出“This is not an A-sequence.”。  试题来源:UFRN-2005 Contest 2 在线测试地址:UVA 10930 提示 将序列中早先出现的数和存储在g[]表中,g[]表的长度为tot;数和产生的标志设为f[],即f[k]标志k是否为序列中早先出现的多个不同项的和;记录当前项为z,前项数为la。 我们依次读入每个数z,若z为已经出现过的数和或者小于前项数(f[z]||z≤la),则输出非A序列的信息并退出计算过程;否则分析g表中的每个数和,若g[i]+z未在g表中出现(!f[g[i]+z]),则将g[i]+z加入g表,并设f[g[i]+z]=true。然后将z设为后项数的前项(la=z),再处理下一项数。 这个过程一直进行到序列中的所有整数都处理完为止。 **【2.4.8 Building designing】** 【问题描述】 一个建筑师要设计一个非常高的建筑物。该建筑物将由若干楼层组成,每个楼层的地板有确定的大小,并且一个楼层地板的大小必须大于它上面楼层地板的大小。此外,建筑师还是一个著名的西班牙足球队的球迷,要在建筑物上漆上蓝色和红色,每个楼层一种颜色,这样,两个连续的楼层的颜色是不同的。 设计有n 层结构的建筑物,每个楼层具有相关的大小和颜色,所有的楼层大小不同。建筑师要在这些限制下设计最高可能的建筑物,使用可用的楼层。 输入: 输入的第一行给出要解决的测试用例数p,每个测试用例的第一行给出可能的楼层的数目,然后每行给出每个楼层的大小和颜色,每个楼层用一个在-999999和999999之间的整数表示,不存在大小为0的楼层,负数表示红色的楼层,正数表示蓝色的楼层,楼层的大小是这个数字的绝对值。不存在大小相同的两个楼层。本题楼层的最大数目是500000。 输出: 对每个测试用例,输出一行,给出在上述条件下最高建筑的楼层数。  试题来源:IV Local Contest in Murcia 2006 在线测试地址:UVA 11039 提示 输入每层楼的大小和颜色,所有楼层按照大小递减的顺序排序。然后将最底层颜色设为蓝色,按照相邻层颜色交替的要求计算最长递减子序列的长度l1;接下来将最底层颜色设为红色,按照相邻层颜色交替的要求计算最长递减子序列的长度l2。 显然,最高建筑的楼层数为max{l1,l2}。 **【2.4.9 Light Bulbs】** 【问题描述】 Hollywood最新的剧院Atheneum of Culture and Movies(ACM)有一个巨大的计算机控制的遮沿,上面有成千上万盏灯。一行灯由一个计算机程序进行自动控制。不幸的是,电工在安装开关时出现了错误,而今晚是ACM的开业式。请编写一个程序,使开关能正常执行。 遮沿上的一排n 盏灯由 n 个开关控制。灯和开关从左到右的编号是从1到n。每个灯泡不是开就是关。每个输入用例给出一排灯的初始情况和希望最后达到的情况。 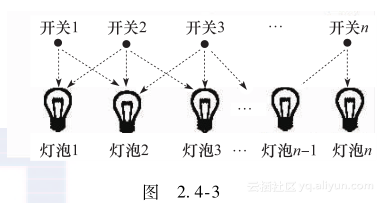 原来的照明计划是让每个开关控制一个灯泡。然而,电工的错误造成每一个开关来控制两个或三个连续的灯泡,如图2.4-3所示。最左边的开关 (i=1) 操控最左边的两个灯泡 (1和2);最右边的开关 (i = n)操控最右边的两个灯泡 (n-1和n),其他的每个开关(1 < i < n)操控三个灯泡:i-1、i和i+1。(特例是只有一个灯泡和一个开关,开关的切换简单地操控灯泡。)也就是说,如果灯泡1开而灯泡2关,则翻转开关1,灯泡1关而灯泡2开着。将一行灯泡从初始的状态转化到最终的状态的最小变化代价是完成这一变化所需要进行的开关最少的翻转次数。 用二进制来表示一排灯的状态,其中0表示灯关,1表示灯开。例如,01100表示有5盏灯,第2盏和第3盏灯开着。通过翻转开关1、 4和5可以把这一状态转换为10000,但也可以简单地翻转开关2,这样代价就小。 请写一个程序求出将一排灯从初始状态转变为最终状态要翻转开关的最小的代价。在某些初始状态和最终状态之间不存在转换。为了表达上的紧凑,采用十进制整数而不是二进制来表示灯泡的状况,即01100和10000分别用十进制数12和16来表示。 输入: 输入包含若干测试用例,每个测试用例一行,每行给出两个非负的十进制整数,至少一个是正数,每个最多100位。第一个整数表示一排灯的最初状态,第二个整数表示这排灯的最终状态。这些整数的二进制数表示这些灯的初始状态和最终状态,1表示灯开着,0表示灯关着。 为了避免前导零问题,本题设定第一盏灯不是在初始状态就是在最终状态是开着的(或者两者都是)。在输入行中,数据的前后没有空格,两个十进制整数没有前导零,初始状态和最终状态由一个空格分开。 在最后一个测试用例后跟着一行,由两个0组成。 输出: 对于每个测试用例,输出一行,给出测试用例编号和一个十进制数,表示将那排灯从初始状态转换到最终状态需要翻转开关的最小代价集合。在这个整数的二进制等价数中,最右边的数字表示第n个开关,1表示开关被翻转,0表示开关没有被翻转。如果无解,输出 “impossible”;如果有多于一个解,则输出等价的最小十进制数。 在两个测试用例之间输出一空行,输出格式如下例所示。  试题来源:ACM World Finals-Beverly Hills-2003 在线测试地址:UVA 2722 提示 每个开关要么翻转要么不动,不可能翻转多次。当第一个开关动作确定之后,只有第二个开关会影响到第一盏灯,所以第二个开关动作也确定了,以此类推可以确定所有开关动作。所以枚举第一个开关是否翻转,然后依次推出后面所有开关动作。由于范围较大,所以用高精度。 **【2.4.10 Link and Pop the Block Game】** 【问题描述】 最近,Robert在互联网上发现了一款新游戏,是最新版本的“连连看(Link and Pop)”。游戏规则很简单。起初的时候,给出n×m的方格板,在板上放满了n×m块方格,每个这样的方格上面都有一个符号。你需要做的就是找到这样一对具有相同符号的方格,这对方格通过最多三条连续的水平或垂直的线段相连。要注意的是,线段不能穿过方格板上的其他方格(图2.4-4给出可能连接的实例,注意一些方格已经从板上删除)。  如果你找到了这样的一对方格,这两个方格就可以被弹出(即被删除)。在此之后,一些方格可以按后面描述的规则移动到方格板上的新的位置。然后,你就开始寻找下一对方格。游戏继续进行,直到方格板上没有方格留下或者不能找到这样的一对方格。 根据下述规则移动方格。首先,每个方格有一个静态的运动属性:“上(up)”、“下(down)”、“左(left)”、“右(right)”和“停着不动(stand still)”。在一对方格被删除后,其他的方格逐一检查,看是否可以朝其运动属性的方向移动。从最上面一行中的方格开始,从上到下逐行检查;在同一行内,从左到右逐个方格检查;如果按方格的移动属性给出方向的相邻位置没有被占据,就将方格移动到这个位置。方格不能移动到方格板的边界之外。当然,方格的属性“停着不动”表示方格留在原来的位置。所有的方格都被检查称为一个检查轮次,在一个检查轮次结束后,下一轮的检查轮次就又开始了。这种情况持续下去,直到按照移动规则,没有方格可以移动到一个新的位置。这里要注意的是,在每个检查轮次中,每个方格被检查,可能移动仅有一次。在一轮检查中,如果一个方格已经被检查了,就不会再被检查了,并移动到一个新的位置。 Robert感到这个游戏非常有趣。然而,在玩了一段时间后,他发现,当方格板的大小很大的时候,找到一对相应的方格就变得非常难。而且,他经常因为没有找到更多的方格对,而得到“Game Over”。Robert认为,这不是他的过错,并不是所有的块都可以被弹出和删除。如果方块最初是随机放置的,那么很可能这场游戏是无解的。然而,通过玩游戏好多次来证明这一点,将是非常耗费时间的。因此,Robert请你为他写一个程序,模拟他在比赛中的行为,来看是否可以完成游戏。 为了使这个程序成为可能,Robert总结了他选择方格对的规则如下。首先,找到可以用一条直线线段相连的一对方格,并将这对方格弹出,因为这类方格对很容易找到。然后,如果这样的方格对不存在,就找到由两条直线线段相连的方格对,并将之弹出。最后,如果上述两种方格对都不存在,就找到由三条直线线段相连的方格对,并将之弹出。如果用相同数量的直线线段连接的方格对多于一对,那么在这些对中选择上方格处于最上方的那一对(如果若干对都有方格块在最上面的一行,则选择在左边的方格块最左边的那一对);如果还是存在若干对(若干对在上方的方格在同一行,在左边的方格在同一列),那么就根据相同的规则比较方格对中的另一个方格。图2.4-5显示了一个遵循上述规则的“连连看”的迷你游戏。  输入: 输入包含不超过30个测试用例。每个测试用例的第一行包含两个整数n, m (1≤n, m≤30),表示方格板的大小。接下来给出n行,每行包含m个由单个空格分隔的字符串。这些字符串各表示一个方格的初始配置。每个字符串由两个大写字母组成。第一个字母是方格的符号,第二个字母是字母'U','D','L','R'和'S',分别表明方格的属性之一:向上、向下、向左、向右和停着不动。在测试用例之间没有空行。输入以两个0(“0 0”)表示结束。 输出: 对于每个测试用例,首先输出测试用例编号。在这一行后,输出n行,每行m个字符,表示方格板的最终情况。如果在一个位置上有一个方格存在,则输出方格的符号。如果在这个位置上没有方格,则输出一个句号来代替。在测试用例之间不输出空行。  试题来源:ACM Shanghai 2004 在线测试地址:POJ 2281,ZOJ 2391,UVA 3260 提示 这是一道模拟题,题目中的时限也比较宽泛,所以按照题目所说的方法,依次检查、消去所有的方块就可以得到解。值得注意的是,在检查两个方块是否可以消去的时候,不同的检查方式在效率上有很大差异。我们采用的是这样一种模拟方法: 找到可以用一条直线线段相连的一对方格;如果这样的方格对不存在,就找到由两条直线线段相连的方格对;如果上述两种方格对都不存在,就找到由三条直线线段相连的方格对。如果有多种可能,则找最上、最左的一对方格,将其消去。 每个方格有上、下、左、右和不动这五个移动属性,任何时候处于其中的一个。在一对方格被删除后,逐一检查其他方格,看是否可朝其移动属性的方向移动。从上到下,从左到右,直到没有方格能动为止。 每次找消去的方格对可以用BFS,队列是双向的:若不需要转弯,则加在队头;若需要转弯,则加在队尾。找到所有转弯次数最少的对后,将最上、最左的一对消去,而之后的移动完全照其模拟即可。虽效率较低,但可在时限内得出解。 **【2.4.11 Packing Rectangles】** 【问题描述】 给出4个矩形块,找出一个最小的封闭矩形将这4个矩形块放入,但不得相互重叠。所谓最小矩形指该矩形的面积最小。 所有的4个矩形的边都与封闭矩形的边相平行,图2.4-6给出了铺放4个矩形的6种方案。这6种方案只是可能的基本铺设方案,因为其他方案能由基本方案通过旋转和镜像反射得到。  可能存在满足条件且有着同样面积的各种不同的封闭矩形,你要输出所有这些封闭矩形的边长。 输入: 输入4行,每行用两个正整数来表示一个给定的矩形块的两个边长。矩形块的每条边的边长范围最小是1,最大是50。 输出: 输出的总行数为解的总数加1。第1行是一个整数,表示封闭矩形的最小面积;接下来的每一行都表示一个解,由整数P和Q表示,并且P≤Q。这些行根据P的大小按升序排列,小的行在前,大的行在后,且所有行都应是不同的。  试题来源:IOI 1995 在线测试地址:POJ 1169 提示 1.求封闭矩形的长和宽 正好能互不重叠地放入4个矩形块的封闭矩形的形式很多。幸好试题总结出了6种基本铺放方案,所有铺放方案可由这6种基本方案通过旋转和镜像反射派生出来。倘若试题不给出这个提示,其难度将会陡增。现在的关键问题是如何求这6种基本铺放方案给出的封闭矩形的面积。设4块矩形分别为: 矩形块w,长和宽分别为w1、w2。 矩形块x,长和宽分别为x1、x2。 矩形块y,长和宽分别为y1、y2。 矩形块z,长和宽分别为z1、z2。 上述定义仅是抽象的逻辑定义,并未指出w、x、y、z具体代表哪一块矩形,矩形块的长和宽值当然也是未知的。我们将这4个逻辑矩形块按基本方案铺放,然后分别沿四周最凸出的某矩形块的边(由表达式求出)作平行边。可构造出一个正好能互不重叠地放入4个矩形块的封闭矩形: 第1种铺放方案如图2.4-7所示。 封闭矩形的长为MAX(w1,x1,y1,z1),封闭矩形的宽为w2+x2+y2+z2。 第2种铺放方案如图2.4-8所示。 封闭矩形的长为MAX(w1,x1,y1)+z1,封闭矩形的宽为MAX(z2,w2+x2+y2)。 第3种铺放方案如图2.4-9所示。 封闭矩形的长为MAX(w1,x1+MAX(z1,y1)),封闭矩形的宽为w2+MAX(x2,z2+y2)。 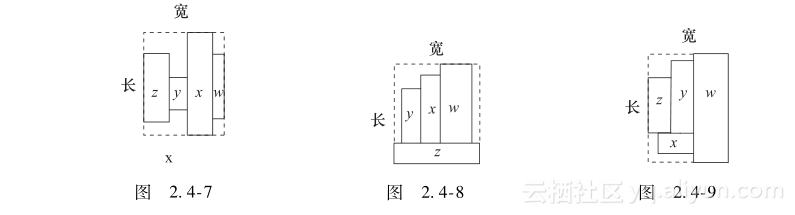 第4、5种铺放方案如图2.4-10所示。 这两种铺放方案有一个共同的特征:两个矩形块叠放在一起,另两个矩形块分别单个铺放。因此可将这两种方案归为一类。 封闭矩形的长为MAX(MAX(w1,x1),y1+z1),封闭矩形的宽为w2+x2+MAX(y2,z2)。 第6种铺放方案如图2.4-11所示。 矩形块w、x、y、z按两行、每行两块的格式,互不重叠地放入一个封闭矩形中。4个矩形块必须同时满足条件z1≥w1,x1≥y1,但是上下各两块的铺放方案有两种互异形式(如图2.4-11所示)。  形式1:封闭矩形的长为MAX(w1+x1,z1+y1),封闭矩形的宽为MAX(w2+z2,x2+y2)。 形式2:封闭矩形的长为MAX(w1+x1,z1+x1),封闭矩形的宽为MAX(w2+z2,x2+y2)。 所有上下各两块的铺放方案都是由上述两种方案通过旋转和镜像反射后得出的。有了封闭矩形的长和宽,则可通过长乘宽得出该矩形的面积。 2.通过枚举法求最小矩形 我们采用枚举法来枚举4块矩形组合这6种基本铺放方案的所有可能情况。枚举的方法是求4块矩形的全排列x1,x2,x3,x4(1≤x1,x2,x3,x4≤4且x1≠x2≠x3≠x4)。 x1对应矩形块w的序号;x2对应矩形块x的序号;x3对应矩形块y的序号;x4对应矩形块z的序号。这样4个逻辑矩形块便一一对应了4个物理矩形块,各矩形块的长和宽也有了确定的值。 每一个4块的全排列按6种基本铺放方案可能产生7个封闭矩形,4!=24个全排列则可产生4!*7=168个可能的封闭矩形。但这只是旋转前的情况。每一个长宽不等的矩形块经旋转90°后铺入,则会产生另一种封闭矩形。因此按照乘法原理,旋转前后共得出4!*7*8=1344个可能的封闭矩形。 相关资源:新年快乐! python实现绚烂的烟花绽放效果